Quantum Resistant Public Key Cryptography

Yongge Wang

We develop post-quantum (or quantum resistant) public key encryption techniques. Our first implementation is based on the Random Linear Code Based Public Key Encryption Shceme (RLCE) which was recently introduced by Dr. Yongge Wang. The full package (including library and C codes for key generation, encryption, and decryption) is available at here: GitHub

Publications

Yongge Wang: Random Linear Code Based Public Key Encryption Scheme RLCE. In Proc ISIT 2016 (pdf)

Yongge Wang: Decoding Generalized Reed-Solomon Codes and Its Application to RLCE Encryption Schemes. Manuscripts 2017. (pdf)

Yongge Wang. Revised Quantum Resistant Public Key Encryption Scheme RLCE and IND-CCA2 Security for McEliece Schemes. (pdf)

Yongge Wang. RLCE Key Encapsulation Mechanism (RLCE-KEM) Specification (pdf)

RLCE Performance

The following Table shows the comparison of the RLCE performance against OpenSSL RSA performance. Both RSA and RLCE were tested with a MacOS Sierra on a MacBook Pro with 2.9 GHz Intel Core i7. The time is in miliseconds.
RSA vs RLCE

RLCE Parameters

The following Table lists the parameters for the RLCE encryption scheme with equivalent AES-128, AES-192, and AES-256 security levels. The Tabble also lists the sizes for the corresponding public key, private key, and message bandwidth
RLCE parameters
where the values in the RLCEpad column are from the following padding scheme
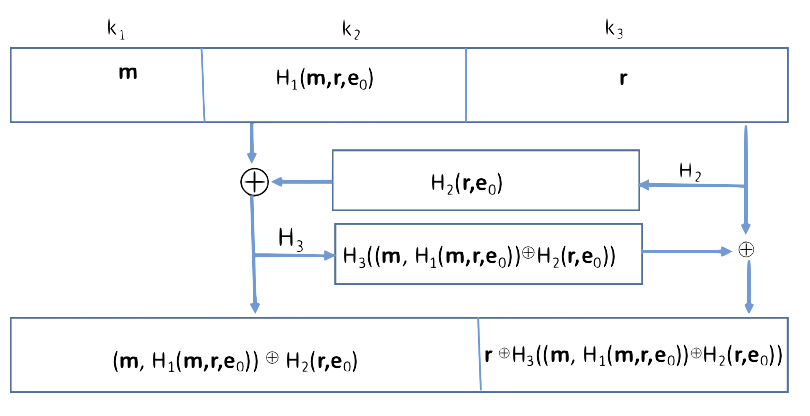
RLCE OAEP pad

Tools and Software for Download

RLCE parameter package: RLCE.jar (19KB). RLCE.jar will test the security strength for given parameters and calculates the padding parameters. It runs on all platforms. For instructions, run: java -jar RLCE.jar
CPP Code for RLCE filtration attack analysis.
The full package (including library and C codes for key generation, encryption, and decryption) is available at here: RLCE.tar.gz

Public keys and ciphertext for you to decrypt

ciphertext: samplecipher
public key: wangpubKey.txt
privafte key wangpriKey.txt